--- Day 9: Jar storage ---
Just as you are about to return to the hotel, Patch shouts:
"Wait! That will never work!"
You turn your head before realising that she was instead talking to the elves packing the jars together, but by that time Patch spots you, and its too late - you're yanked back in.
The elves had spent the evening preparing and packaging the soup jars into boxes. Each box was coated in a quick-acting adhesive, meant to keep them from sliding off the sleigh. Simple - but only if the boxes stayed put long enough to stick.
The head packaging elf, a stout fellow with spectacles perpetually sliding down his nose, waved a dismissive hand. "Nonsense!" he said. "We've done it this way for years. A few boxes won't fit? No problem - we'll just use the next sleigh!"
Patch demanded to see their packing plan, and he obliged, muttering something like "If it makes you leave quicker...". You take a peek at the plans too, and quickly realise that the layout is completely impractical, even from the first few packages. You're suddenly glad you stayed to ensure it all went smoothly.
Patch seemed infuriated. "The next sleigh? There's got to be at least a hundred packages that won't fit! You do realize we have a finite number of reindeer, right?!"
The elves seemingly wouldn't hear it. Patch sighed, folding her arms. "I was afraid of this. But you know these elves. Once they get an idea in their heads, it's impossible to dislodge."
You suspect this might have something to do with the recent hacking attack, and suggest to Patch that if you can show how few packages will actually be able to fit, maybe you can get the elves to see reason.
The input file contains a newline-separated list of jar packages, each represented as a string of the following four values in order, separated by space:
- Type: either
N(normal) orF(fragile), - Drop position: The x coordinate at which to place the left side of the package.
- Width: Decimal width of the package
- Height: Integer height of the package
The package placement starts with an empty area and a floor at y = 0. Packages are placed sequentially in the order given in the input, and each package is placed at its drop position along the x-axis. The package is positioned at the highest possible height such that it rests on the floor or on one or more packages below it. A package may rest partially on multiple packages.
For each package, determine if placing it would cause any packages to topple. If it wouldn't, place it and continue as normal, noting the number of the package (starting at 1, including packages that would topple the tower when counting). If it would, do not place it.
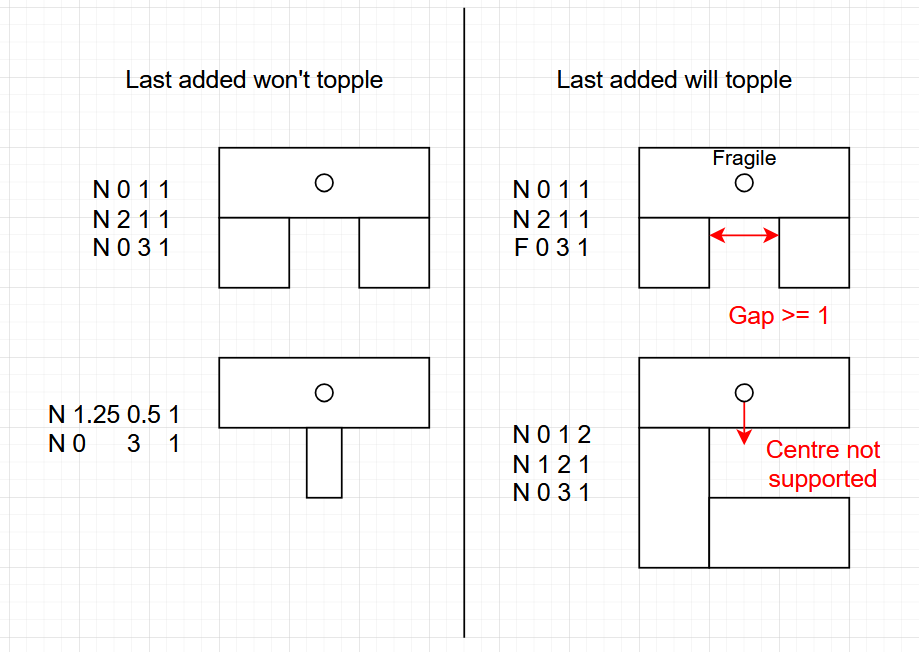
A package will topple the tower if either of the following conditions occur:
- Center of mass is outside supported region
- If the package is on the floor, it is supported.
- Compute the center of mass of the newly placed package alone (which is just its center).
- Determine its supported region, defined as the horizontal span from the leftmost point of the leftmost package directly touching it from below to the rightmost point of the rightmost package directly touching it from below.
- If the center of mass is not within this supported region, the newly placed package causes a topple.
- The rest of the tower can be assumed to be rigid and does not need to be checked for balance, thanks to the time activated adhesive that the packages are coated in - which will harden by the time the next package is placed.
- Fragile gap
- If the package is fragile, check its bottom edge.
- If there is a horizontal gap of length 1.0 or more (along the bottom edge) where it isn't resting on the floor or another package, it breaks and causes a topple.
Bear in mind that the simulation may end up forming multiple towers in different positions.
Can you find the list of package numbers that won't cause a topple when stacked in this sequence? Give your answer as an ascending comma separated list. Expect a somewhat large number of packages.
Example input:
N 7.2 2.9 3
F 9.6 4.3 5
F 11.0 3.0 4
F 12.9 1.7 2
N 12.3 4.2 3
N 19.1 4.0 3
F 5.3 1.6 2
F 10.9 3.7 1
N 15.9 3.7 2
F 2.6 3.8 5
N 18.6 3.5 2
N 5.4 5.0 3
F 8.1 1.7 3
N 15.3 4.2 1
F 8.3 4.4 1
N 8.3 4.2 1
N 10.0 1.7 5
N 9.9 2.3 4
N 16.9 3.1 3
N 15.9 3.7 4
Output:
1,3,4,5,6,7,11,12,13,16,17,18
Explanation:
- Package 2 toppled as it centre of mass was not between supports (COM: 11.8)
- Package 8 broke due to a gap of length>=1 beneath it (between 10.9 and 14.6)
- Package 9 toppled as it centre of mass was not between supports (COM: 17.8)
- Package 10 toppled as it centre of mass was not between supports (COM: 4.5)
- Package 14 toppled as it centre of mass was not between supports (COM: 17.4)
- Package 15 broke due to a gap of length>=1 beneath it (between 8.3 and 12.7)
- Package 19 toppled as it centre of mass was not between supports (COM: 18.4)
- Package 20 toppled as it centre of mass was not between supports (COM: 17.8)
 Download package placement data
Download package placement data